حل معادله گرما با روش دینامیک سیالات محاسباتی (روش crank nicolson) در فرترن

مقدمه

معادله گرما، که به توصیف انتقال حرارت در مواد مختلف می‌پردازد، و در بسیاری از عرصه‌های مهندسی از جمله مکانیک، شیمی و علوم مواد کاربرد دارد. روش Crank-Nicolson به عنوان یکی از تکنیک‌های کارآمد و دقیق در حل معادله گرما شناخته می‌شود. زیرا ترکیبی از روش‌های ضمنی و نیمه‌ضمنی را ارائه می‌دهد که منجر به پایداری و دقت بیشتر در نتایج می‌شود. در این تحقیق، ما به پیاده‌سازی این روش در زبان برنامه‌نویسی فرترن خواهیم پرداخت، شامل تعریف شرایط اولیه و مرزی، ساخت ماتریس‌ها و انجام محاسبات عددی برای تحلیل انتقال حرارت. هدف این مطالعه، بررسی عملکرد روش Crank-Nicolson در شبیه‌سازی پدیده‌های حرارتی و ارائه بینش‌های کاربردی در حوزه دینامیک سیالات محاسباتی است.

توضیحات

این روش شامل گام زمانی با دقت مرتبه دوم و به صورت ضمنی می‌باشد و از لحاظ عددی پایدار است. برای معادلات نفوذ (و بسیاری دیگر از معادلات) می‌توان اثبات کرد که روش کرنک نیکلسون crank nicolson به صورت بی قید پایدار است. با این وجود حل تقریبی آن در صورتی که نسبت گام زمانی به مربع گام مکانی بزرگ باشد (عموماً بزرگتر از نیم) می‌تواند شامل نوسانات قابل توجهی در حل عددی باشد. یکی از روش‌های بسیار پرکاربرد در شبیه سازی معادلات گرما می‌باشد.

هدف از انجام این پروژه حل معادله گرما با روش دینامیک سیالات محاسباتی (روش crank nicolson) و مقایسه ی نتایج حاصل از آن با حل دقیق می باشد. لازم به ذکر تمامی پروژه به کمک زبان برنامه نویسی فرترن انجام شده است.

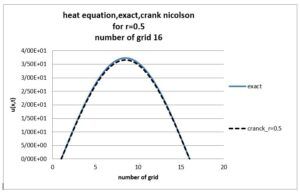
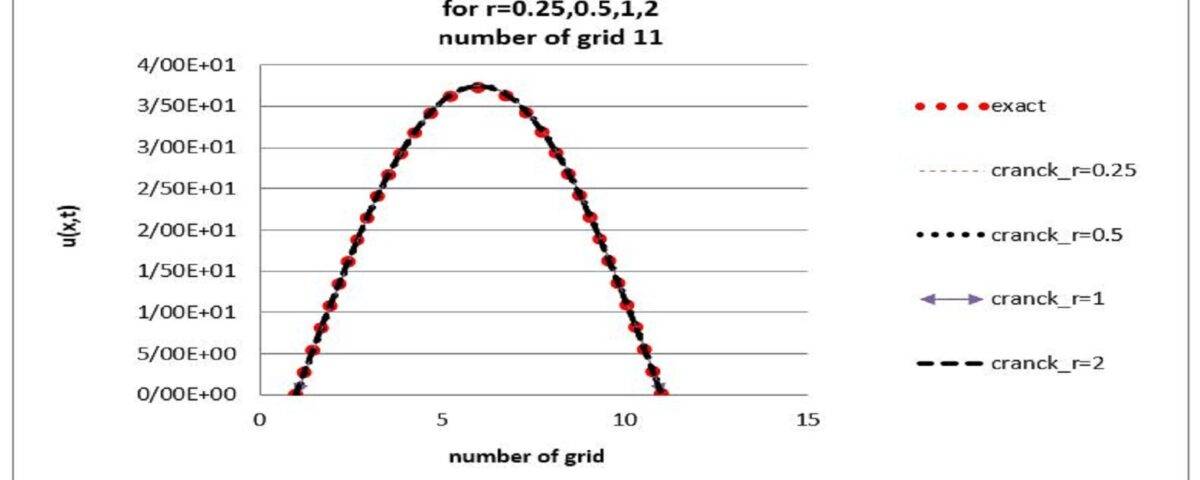
نتیجه گیری

روش Crank-Nicolson، که ترکیبی از دقت و پایداری را ارائه می‌دهد، امکان تحلیل دقیق‌تر فرآیندهای انتقال حرارت را فراهم آورد. با استفاده از شرایط اولیه و مرزی مشخص، شبیه‌سازی‌هایی انجام شد که رفتار حرارتی سیستم را در زمان‌های مختلف نشان داد.

این پروژه نه تنها به بیان اهمیت استفاده از روش‌های عددی در تحلیل مسائل حرارتی کمک کرد، بلکه ابزارهای مفیدی برای پژوهش‌های آتی در زمینه دینامیک سیالات محاسباتی و انتقال حرارت ارائه داد. به طور کلی، این مطالعه بر پتانسیل‌های کاربردی این روش در مهندسی و علم مواد تأکید می‌کند و راه را برای بررسی‌های بیشتر در زمینه‌ مسائل پیچیده‌تر باز می‌کند.