مقدمه
معادله برگر، که به آن معادله جابجایی نیز گفته می‌شود، یک مدل ریاضی مهم در دینامیک سیالات محاسباتی (CFD) است. این معادله برای مطالعه انتشار موج‌های غیرخطی، آشفتگی‌ها و تشکیل موج‌های شوک استفاده می‌شود. این پروژه به حل شکل خطی و غیرخطی معادله برگر می‌پردازد و از روش‌های گسسته‌سازی تفاضل محدود برای شرایط اولیه پیوسته و ناپیوسته بهره می‌برد. هدف این پروژه ارائه راه‌حل جامع و کاربردی برای این مسئله مهم در دینامیک سیالات است.
روش‌های عددی مورد استفاده
برای دستیابی به نتایج دقیق، در این پروژه از چهار روش عددی پیشرفته استفاده شده است و برای حل جنبه‌های مختلف معادله برگر مناسب هستند:
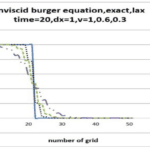
- روش لکس (Lax Method): این روش گسسته‌سازی تفاضل محدود برای حل معادلات دیفرانسیل جزئی هایپربولیک مناسب است و به عنوان مبنایی برای مقایسه با سایر روش‌ها به کار می‌رود.
- روش تفاضل بالادست (Upwind Differencing Method): این روش برای حل پدیده‌های جابجایی مناسب است و با کاهش نفوذ عددی، ناپیوستگی‌های شرایط اولیه را به‌خوبی حل می‌کند.
- روش لکس-وندروف کلاسیک (Classical Lax-Wendroff Method): یک روش دقیق با مرتبه دوم که با استفاده از مشتقات زمانی و مکانی، دقت را بهبود می‌بخشد و برای حل نرم‌تر معادلات غیرخطی کاربرد دارد.
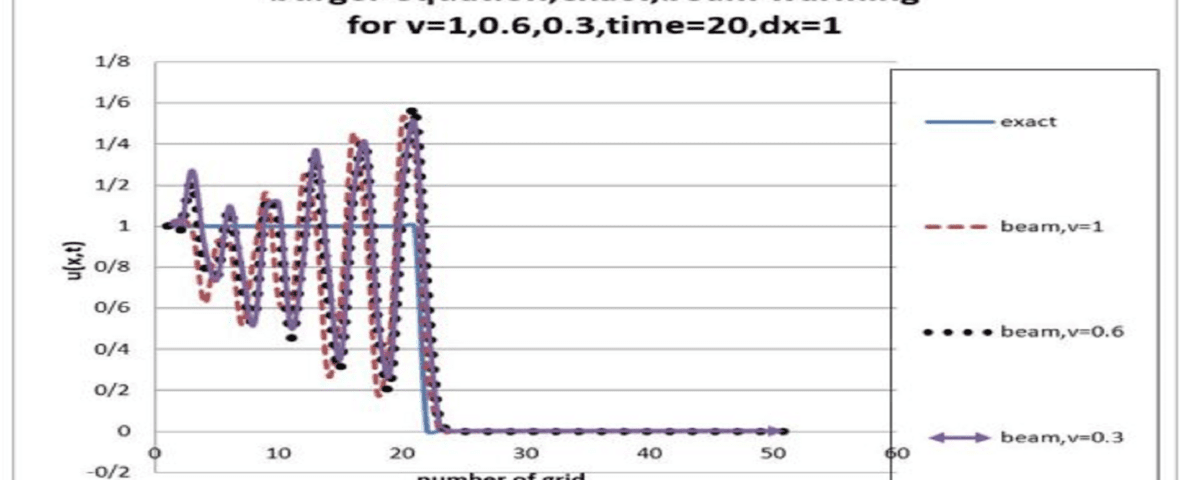
- روش بیم-وارمینگ (Beam-Warming Method) – مرکز زمانی یا به‌صورت ضمنی: این روش ضمنی با گام‌های زمانی بزرگتر پایدار است و برای حل معادلات غیرخطی، مانند معادله غیرخطی برگر، مناسب می‌باشد.
هدف پروژه
هدف اصلی این پروژه حل معادله برگر با استفاده از روش بیم-وارمینگ و مقایسه نتایج آن با حل دقیق است. این مقایسه امکان ارزیابی دقت و عملکرد این روش را در به تصویر کشیدن دینامیک معادله فراهم می‌کند.
پیاده‌سازی پروژه با زبان فرترن
تمامی الگوریتم‌های حل در این پروژه با استفاده از زبان برنامه‌نویسی فرترن، که به دلیل کارایی بالا در محاسبات علمی شناخته شده است، پیاده‌سازی شده‌اند. با تهیه این پروژه، شما به کد کامل فرترن برای هر روش، به همراه فایل‌ها و نتایج مربوطه دسترسی خواهید داشت.
ویژگی‌ها و خروجی‌های کلیدی
- دسترسی به کد کامل تمامی روش‌ها: کد فرترن برای روش‌های لکس، تفاضل بالادست، لکس-وندروف و بیم-وارمینگ در اختیار شما قرار می‌گیرد.
- مقایسه نتایج: مقایسه دقیق نتایج با حل تحلیلی برای ارزیابی عملکرد و دقت هر روش.
- مستندسازی کامل: کدهای هر بخش به‌خوبی مستندسازی شده‌اند تا درک و تطبیق آنها برای سایر معادلات و شرایط اولیه آسان‌تر باشد.