Description
The wave equation is a partial differential equation that describes the behavior of waves in space and time. This equation has many applications in various branches of physics, including mechanics, acoustics, electromagnetism, and quantum physics.
General Form of the Wave Equation
The general form of the wave equation in one spatial dimension is as follows:
∂²u/∂t² = c² ∂²u/∂x²
where:
- u(x, t): The value of the disturbance (such as displacement, pressure, electric field) at point x and time t.
- c: The speed of wave propagation.
- ∂²u/∂t² and ∂²u/∂x²: Second-order partial derivatives of u with respect to time and space, respectively.
Types of Wave Equations
The wave equation is a mathematical equation that describes the behavior of waves in space and time. Depending on the medium in which the wave propagates, the wave equation takes on different forms.
Classification of Wave Equations Based on Spatial Dimension
Wave equations can be classified into three categories based on the number of spatial dimensions in which they are defined:
-
One-dimensional wave equation:
This equation is used to describe waves that propagate in a straight line. Examples of such waves include waves on a stretched string, sound waves in a narrow tube, and waves in a spring.
-
Two-dimensional wave equation:
This equation is used to describe waves that propagate on a two-dimensional surface. Examples of such waves include waves on the surface of water, waves in a drum, and waves in a thin membrane. The general form of the two-dimensional wave equation is:
∂²u/∂t² = c² (∂²u/∂x² + ∂²u/∂y²)
-
Three-dimensional wave equation:
This equation is used to describe waves that propagate in a three-dimensional space. Examples of such waves include sound waves in air, light waves, and electromagnetic waves. The general form of the three-dimensional wave equation is:
∂²u/∂t² = c² (∂²u/∂x² + ∂²u/∂y² + ∂²u/∂z²)
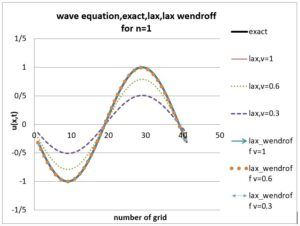
The purpose of this project is to solve the wave equation with the computational fluid dynamics method (Lax, Lax Wendroff methods) and compare the results with the exact solution. Lax, Lax Wendroff method, named after Peter Lax and Burton Wendroff. A numerical method for solving hyperbolic partial differential equations is based on finite differences. This method is an example of explicit time integration, where the determinant function of the governing equation is evaluated at the current time. It should be mentioned that the entire project has been done with the help of Fortran programming language. By preparing this project, the code of all the methods along with the results will be available to you.