Introduction
As an emerging field, micro process engineering has a high potential for process improvement. This improvement is due to the high surface-to-volume ratio and the improved safety of the processes. In this context, the replacement of large structures and discontinuous processes with small and continuous units, especially in the chemical and pharmaceutical industries, has brought positive results.
While small-scale reactors, mixers and heat exchangers are well developed, small-scale fluid separation equipment is not yet mature enough to be used in production units. In particular distillation, as one of the most important separation processes for homogeneous liquid mixtures, needs to be scaled down. One of the main obstacles in this field is the lack of essential design principles.
One promising concept for small-scale distillation is zero-gravity distillation (ZGD). By using the heat pipe principle, it is possible to realize the stable and reciprocal flow of liquid and vapor phases. Compared to conventional distillation units, capillary forces are used to make liquid flow in ZGD units. This feature allows the ZGD unit to be used in space and under low gravity conditions.
In the present project, based on the data and information of Wende et al.’s paper, we have presented a predictive model for ZGD simulations with metal foams. This model includes feed streams, bottom product and distillate streams, heat conduction in the walls of ZGD unit and pressure change due to phase change. Metal foams are chosen due to their high porosity and permeability and large specific surface area. Also, these foams are commercially produced and widely available.
Types of Micro Distillation
Micro Distillation Under Centrifugal Force
In micro-distillation, due to the high ratio of surface to volume, the effect of gravity against surface forces is less. However, research has been done based on the possibility of designing a micro-distillation device based on centrifugal forces. In this method. the centrifugal acceleration component directs the liquid to the outside of the spiral. And the vapor phase can flow inward by adjusting the pressure gradient.
The vapor phase moves towards the cold end due to the pressure gradient. It is enriched in the more volatile component and becomes less enriched in the volatile component as the liquid phase moves towards the hot end. Light and heavy products are removed from the column at the end of the stage.
Microdistillation Using Split Flow
In this micro-distillation process, the mixture of liquid and gas is introduced into a helical microchannel,. where liquid evaporation occurs and a non-equilibrium state between the liquid and gas phases is created. The carrier gas, usually nitrogen or noble gases, drives the resulting vapors through the channel.
These vapors reach a membrane micro-separator that performs the separation process based on capillary forces. The liquid phase that wets the porous membrane. It is transferred to another outlet through the pores of the membrane. While the gas phase carrying steam passes through the membrane and reaches a separate outlet. This process leads to the separation of enriched vapors from the initial mixture. each of which is retrieved from two different outputs respectively.
Micro Distillation Using Membrane and Vacuum
This method includes microfluidic channels that are located in different layers and through which the flow of liquid and vapor moves in order to carry out the distillation process. The liquid feed enters the distillation channel and is heated under the influence of a hot plate. Due to the hydrophobic nature of the PTFE membrane, the produced steam penetrates into the steam channel only through the dry pores of the membrane.
Then the vapor moves to the left and condenses to some extent. This process causes mass exchange between the liquid and vapor phases through the membrane, which ultimately results in the separation of the heavier and more volatile components.
Micro-Distillation in Zero Gravity Using a Heat Pipe
In this method, a heat pipe is used to separate liquid mixtures. First, the feed enters the channel and in the evaporation zone, the liquid heats up to a certain temperature and vaporizes. The steam produced in the adiabatic transport zone is transferred and condensed to the condenser section due to the pressure difference.
The condensed liquid is returned to the heating section using capillary force in the porous walls. No need for gravity. In steady state, this device creates a general reflux and more volatile components are separated in the condenser and less volatile components in the evaporator. And a continuous distillation is possible without the use of gravity.
Mathematical Model of Zero-Gravity Distillation Unit (ZGD)
In this section, a mathematical model is presented to describe the ZGD unit. In this model, a device filled with a two-phase system including vapor and liquid is considered. Both phases contain binary mixtures of two similar compounds. liquid is placed inside metal foam, which is surrounded by a layer of vapor.
ZGD unit consists of an evaporator on the left side and a condenser on the right side. feed stream enters from middle of the device and moves down along x-axis. Distillate and bottom product streams are taken from liquid phase from evaporator and condenser.
The Initial Design of The Computing Domain
In this model, it is assumed that the capillary forces in the metal foam are strong enough to immediately compensate the displacement of the phase surface. This hypothesis leads to a certain surface for the liquid-vapor phase, which corresponds to the boundary between the metal foam and the vapor.
Fluid Dynamics in the System
It is not possible to perform direct numerical simulation to describe the fluid dynamics of this system due to the existing complexities. On the one hand, the structure of metal foam is irregular and its actual geometry is unknown. On the other hand, it is not possible to analyze the fluid flow in the pores of the entire device for a reasonable time due to the strong interplay of momentum, heat and mass transfer.
Therefore, the concept of hydrodynamic similarity (HA), which was first proposed by Kenig in 1997, is used. The main idea of this concept is to replace the real complex flow with a combination of simplified flow patterns. These models allow for a more accurate description of heat and mass transfer. HA models have been successfully used in various separation processes.
Model Assumptions
In this model, both fluids are considered as Newtonian fluids with constant fluid properties. External forces such as gravity are neglected. The vapor phase flow is simplified as a creep flow. whose flow is stable, calm and parallel to the phase surface. Under these conditions, the Navier-Stokes equation for the vapor phase is written as follows:
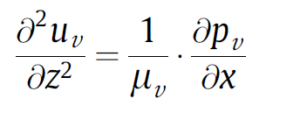
The motion of the liquid phase is described as plug flow through Darcy’s law to account for the effect of the metal foam on the flow:
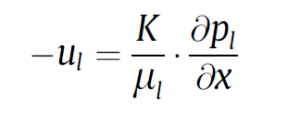
Here, K is the permeability, an empirical parameter depending on the structure of the metal foam. As the boundary conditions for the first equation, the no-slip condition on the upper wall and the Drichlet boundary condition, uV=0, are applied on the surface of the liquid-vapor phase. Heat transfer by a steady flow is described by the two-dimensional formulation:
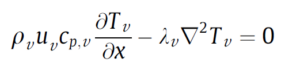
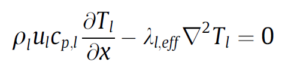
The effective thermal conductivity in the metal foam-liquid region, λl,eff, depends to a large extent on the properties of the metal foam. A valid empirical correlation for effective heat conduction is proposed by Bhattacharya et al.:
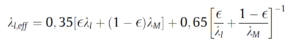
Fourier Law
The heat fluxes qF, qB, qD of the feed and product streams are considered in the boundary conditions for the equation. In the values of XB, XD, XF, which are related to the feed and product withdrawal positions, the following relationships hold (Fourier’s law):
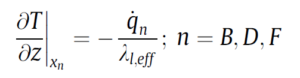
Heat fluxes using the respective specific enthalpies hB,l, hD,l, hF,l and with the mass flow rate B, D and F of the respective flows:
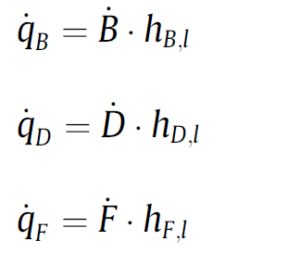
There is no thermal accumulation at the surfaces between the walls and the fluid phases, and therefore, all heat fluxes perpendicular to the wall surface must be equal.
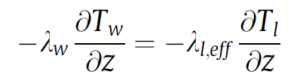
The boundary condition between the upper wall and the vapor phase is:
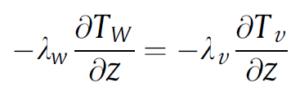
The left and right walls are in contact with both the liquid phase (below the liquid-vapor surface) and the vapor phase (above the surface). Therefore, the relevant wall-fluid boundary conditions should be divided according to the dimensions and dimensions of the porous layer, i.e.,
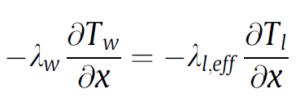
for the liquid phase
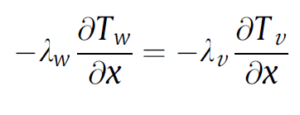
for the vapor phase. The only heat transfer mechanism in the wall is conduction. Then, the transfer equation for the wall becomes:
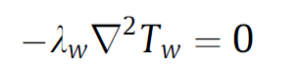
Heat flux for Evaporator and Condenser
The boundary condition at the transition from the wall to the periphery is a zero-gradient condition, since the unit is assumed to be adiabatic. In the lower wall, the heat fluxes are considered for the evaporator and condenser. Regarding the performance of the feed and recovery streams, qE and heat flux from the ZGD unit were removed by the condenser qC. which is determined by equalizing the evaporator and condenser:
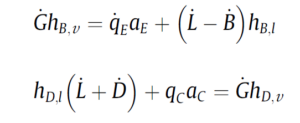
All equations were implemented in MATLAB software and verified using finite difference method. They were solved sequentially and iteratively. The computation domain in the xz-plane is confirmed by a non-uniform grid distribution with 1600 nodes in the X-direction and 900 nodes in the Z-direction.
Simulation Results and Discussion
This section presents the results of numerical simulations and validates the developed mathematical model with experimental data. It should be noted that the properties of the compounds were extracted with the help of Span Plus. This validation has been done through two parameter studies performed in zero gravity distillation (ZGD) processes with full reflux. In the first study, the effect of different wall materials was investigated and in the second study, the initial composition of the separated mixture was changed.
Validation
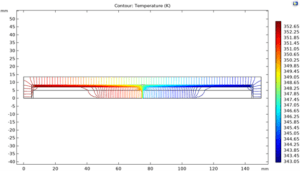
The studied unit had an internal length of 140 mm and a height of 3.5 mm. height of the metal foam made of chromium-nickel alloy with thermal conductivity of 114 W/m.kλ and porosity of 0.96 was equal to 2 mm. The walls of unit were also made of brass with a thickness of 5 mm and a thermal conductivity of 90 W/m.kλ.
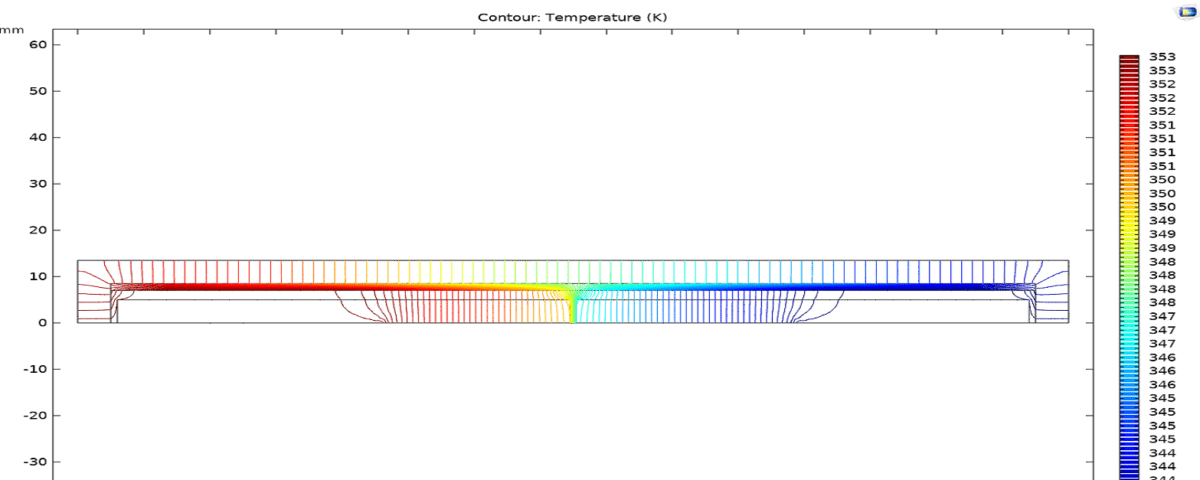
All these parameters were applied in the model. The simulation results, including temperature distribution, flow rate and n-hexane mass fraction, are presented in the figure below. The results showed that the heat flux stored in the evaporator leads to evaporation and the heat flux removed in the condenser leads to condensation. These phase changes lead to steam flow in the positive direction of the x-axis and a decrease in flow velocity due to the dominant condensation after the maximum velocity point. The liquid flow has a similar behavior in the negative direction of the x axis.
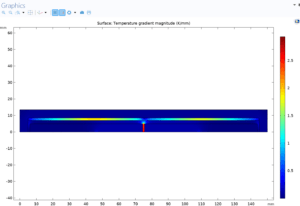
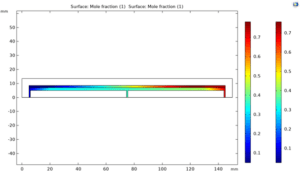
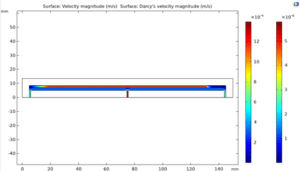
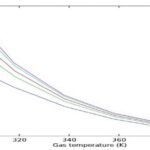
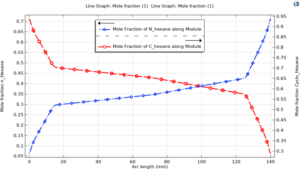
The figure below shows the simulated mole fractions of n-hexane in the liquid phase along the x-axis. Comparison of these values with experimental data shows a good agreement.
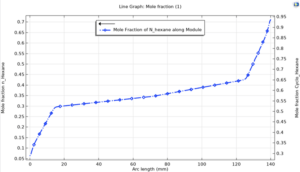
View Results
A new predictive model was developed for the simulation of ZGD units based on the concept of hydrodynamic similarity. This model controls the coupled transport phenomena in the ZGD unit and the effect of phase change on the internal pressure profile. In addition, the thermal conductivity of the walls of the ZGD unit and the feed, distillate and bottom product streams were also considered in the simulation.
The developed model was validated with experimental data related to ZGD with full backflow, and the simulated results were in good agreement with the experimental values. Next, the influence of the wall material and the initial composition of the mixture was investigated. The results showed that the use of copper instead of brass as the wall material increases the separation efficiency, and due to the higher thermal conductivity of copper, more severe changes in the concentration profile were observed.
Other Results Obtained
Thermal Flux
And the heat flux changes in the evaporator and condenser were accurately simulated.
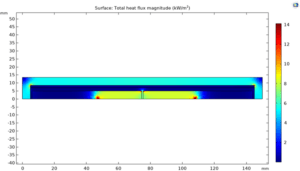
Temperature Gradient at The Surface

Mole Fraction of Material in Metal Foam
And the distribution of mole fraction of materials in metal foam was carefully investigated and reasonable results were obtained.
Antoine Pressures of Materials at The Interface of Two Phases
And the pressures calculated using Antoine equation for different phases were compared with the experimental data.
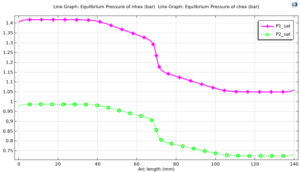
Total Fluid Pressure at The Interface
The total fluid pressure at the interface was correctly calculated using the developed model.

Calculated Equilibrium Mole Fraction at The Interface for The Gas Phase
And the results showed a good agreement with the experimental data.
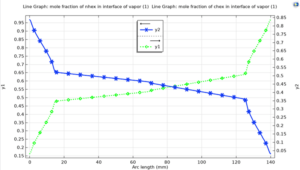
The Sum of Calculated Mole Fractions
The results of the total mole fractions calculated in the interface show the high accuracy of the model.
Modeling and Simulation of Gravityless Distillation With Foam
In this project, the modeling and simulation of gravity-free distillation unit with metal foams was done in Comsol software version 5.6 based on the information of the article and the operational parameters were analyzed. This project comes with full training.