Introduction
The design and optimization of various mechanical systems require extensive testing and experimentation. These tests and subsequent redesigns are often costly and time-consuming, presenting significant challenges in the design and manufacturing processes. As computational power has advanced, engineers have increasingly turned to simulation to model different mechanical processes. A prime example of this is the simulation of fluid flow fields using the science of Computational Fluid Dynamics (CFD).
CFD allows engineers to visualize and analyze fluid behavior within a system, ultimately leading to better designs and more efficient processes. This project aims to solve the Burgers’ Equation in a steady state using CFD methods such as FTCS (Forward Time Centered Space), Upwind, and Leonard methods, comparing the results obtained with exact solutions. All aspects of this project are implemented using Fortran programming, providing users with comprehensive access to the source code and results.
Understanding the Burgers’ Equation
What is Burgers’ Equation?
Burgers’ Equation is a fundamental partial differential equation from fluid dynamics and applied mathematics. It describes the motion of a fluid and can represent various phenomena, such as shock waves and turbulence. The equation can be linear or nonlinear, with the nonlinear form exhibiting complex behavior, such as shock formation and wave propagation.
Importance of Solving Burgers’ Equation
Solving Burgers’ Equation is vital for understanding complex fluid behaviors. It serves as a simplified model for more complex fluid dynamics problems, allowing researchers to develop numerical methods and enhance their understanding of shock formation and turbulence in various systems. Furthermore, solutions to Burgers’ Equation are essential for practical applications in engineering, meteorology, and environmental studies.
Numerical Methods for Solving Burgers’ Equation
Computational Fluid Dynamics (CFD)
CFD utilizes numerical analysis and algorithms to solve and analyze fluid flow problems. By discretizing the equations governing fluid motion, CFD enables engineers to simulate real-world fluid behavior under various conditions. The increasing computational capabilities of modern computers have made CFD a preferred tool for engineers and researchers.
Overview of Numerical Methods
In this project, three numerical methods are utilized to solve the steady-state Burgers’ Equation:
- FTCS Method: The Forward Time Centered Space (FTCS) method is a simple finite difference method that discretizes the time and spatial dimensions. It is particularly useful for solving linear equations and provides a straightforward implementation.
- Upwind Method: This method is designed to handle advection-dominated problems. By using information from the upstream direction, it reduces numerical dispersion and provides better stability for solving Burgers’ Equation.
- Leonard Method: This method is a more advanced finite difference technique that combines elements of the FTCS and Upwind methods. It aims to enhance accuracy while maintaining stability, making it suitable for nonlinear equations like Burgers’ Equation.
Project Implementation in Fortran
Setting Up the Project
The project is implemented using Fortran, a powerful programming language known for its efficiency in numerical computing. The choice of Fortran allows for optimized performance in executing complex calculations associated with fluid dynamics.
Discretization of Burgers’ Equation
The first step in the implementation involves discretizing the Burgers’ Equation using the selected numerical methods. This process transforms the differential equation into algebraic equations, which can be solved iteratively over small time and spatial steps.
Initial and Boundary Conditions
Defining initial and boundary conditions is critical for accurately solving the Burgers’ Equation. The initial conditions specify the velocity and pressure fields at the beginning of the simulation, while boundary conditions define the behavior of the fluid at the edges of the simulation domain. Properly setting these conditions significantly impacts the simulation results and their accuracy.
Implementation of Algorithms
The core algorithms for each method are implemented in Fortran, allowing for efficient computation. The algorithms are structured to handle the time-stepping and spatial discretization required to evolve the fluid state over time accurately.
Analyzing Results and Comparisons
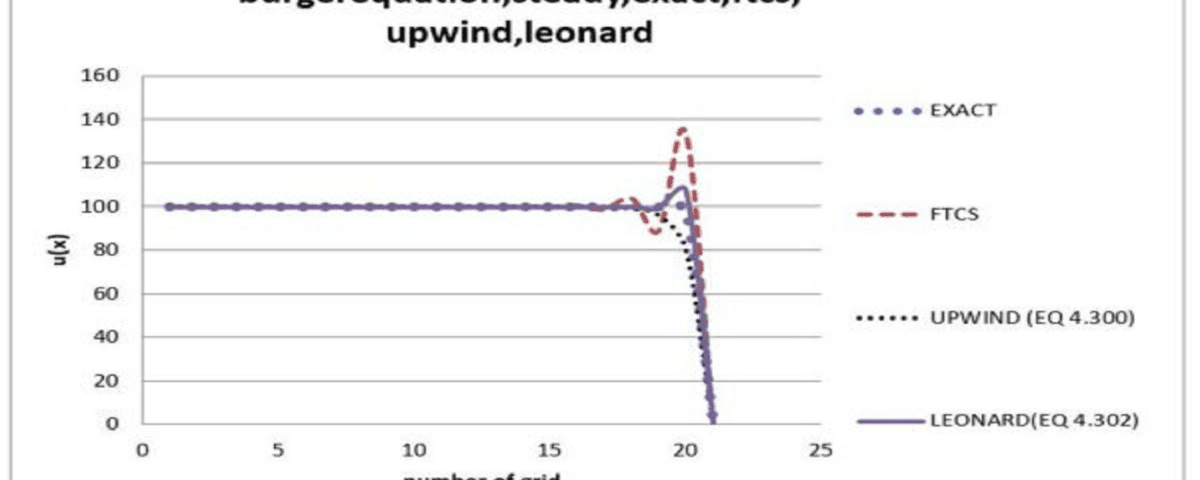
Once the simulations are complete, the results obtained from the numerical methods are compared to exact solutions of the Burgers’ Equation. This comparison is essential for assessing the accuracy and performance of each numerical method, helping to identify strengths and weaknesses in the approaches.
Advantages of Numerical Methods in CFD
- Efficiency: Numerical methods allow for rapid simulations of complex fluid flows, significantly reducing the time and cost associated with physical testing.
- Flexibility: CFD techniques can be adapted to a wide range of fluid dynamics problems, from simple flow fields to complex interactions in turbulent systems.
- Insightful Visualization: CFD provides powerful visualization tools, enabling engineers and researchers to understand fluid behavior better through graphical representations of flow patterns, pressure distributions, and other key parameters.
- Predictive Capabilities: By modeling fluid dynamics using numerical methods, engineers can predict system behavior under various operating conditions, leading to more informed design decisions.
Key Findings and Results
Access to Full Fortran Code
This project provides complete access to the Fortran code for all numerical methods utilized. This transparency enables users to understand the implementation details and modify the code according to their specific requirements.
Simulation Results
The results obtained from the simulations are presented in various formats, including tables and graphs. These visual representations facilitate easy interpretation of the outcomes and provide a clear comparison between the numerical methods and exact solutions.
Comprehensive Documentation
Detailed documentation accompanies the project, covering all implementation steps and analysis processes. This documentation is designed to support users in understanding the methodology and applying the techniques to other fluid dynamics problems.
Conclusion
This project represents a significant effort to explore the solution of Burgers’ Equation using various numerical methods in CFD. By providing clear insights into the implementation, results, and advantages of these methods, it serves as a valuable resource for students, researchers, and engineers interested in fluid dynamics. The findings contribute to a deeper understanding of numerical approaches in solving complex fluid flow problems, ultimately enhancing the design and optimization processes in mechanical engineering.
Future Work and Recommendations
This project lays the groundwork for further research in CFD and fluid mechanics. Future work could explore additional numerical methods, such as Lax-Wendroff and higher-order schemes, to improve accuracy and stability. Moreover, expanding the scope to include more complex fluid dynamics scenarios will enrich the learning experience for users and contribute to advancements in the field.