Introduction
Computational Fluid Dynamics (CFD) is a vital branch of fluid mechanics that employs numerical analysis and advanced algorithms to model and analyze fluid flows and their related phenomena. This approach enables the solution of complex differential equations governing fluid behavior using numerical methods. One common application of CFD is the solution and analysis of Burgers’ Equation, which has been implemented in this project using the Forward Time, Centered Space (FTCS) method with Fortran programming.
Overview of Burgers’ Equation
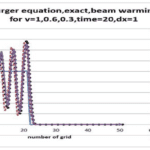
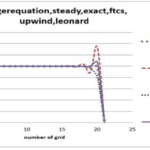
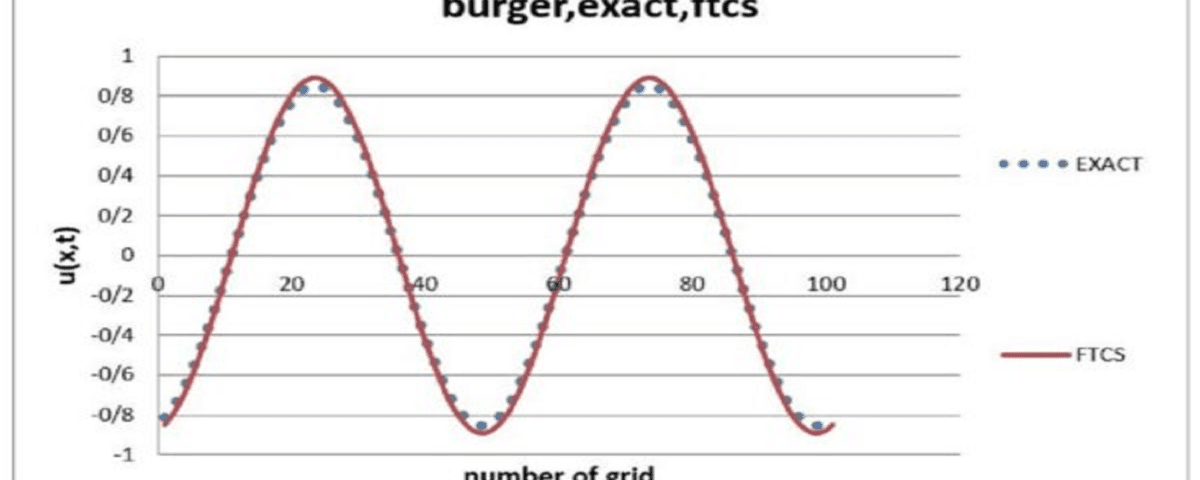
Burgers’ Equation is a significant mathematical model in fluid dynamics and mathematical modeling that studies nonlinear flows and wave propagation in fluid environments. This equation is utilized in analyzing phenomena such as turbulence, nonlinear flows, and shock wave formation in fluids. In this project, Burgers’ Equation is solved using the FTCS numerical method, and the results are compared to the exact solution of the equation.
Numerical Methods and Implementation in Fortran
To solve Burgers’ Equation in this project, the FTCS numerical method has been employed. FTCS is a finite difference discretization method that uses a forward time approach and a centered spatial approach. Despite its simplicity, this method allows for the analysis of fluid behavior over short time steps. The implementation of this method has been carried out in Fortran, which is well-suited for scientific computations due to its high efficiency and capability in handling CFD problems.
Project Steps
Discretization of Burgers’ Equation
Initially, Burgers’ Equation is discretized using the FTCS method. This process involves converting the differential equation into algebraic equations, which are then solved at small time and spatial increments.
Definition of Initial and Boundary Conditions
Initial and boundary conditions are precisely defined for the equation. These conditions include the initial velocity and pressure of the fluid, as well as the conditions at the edges of the study domain, significantly impacting the simulation results.
Algorithm Implementation in Fortran
Using Fortran, the code related to solving Burgers’ Equation with the FTCS method is written, and simulations are conducted at specified time increments. This program provides accurate computations and high processing speed for larger models.
Results Analysis and Comparison with Exact Solutions
After performing the simulations, the results obtained from the FTCS numerical method are compared with the exact solution of the equation to evaluate the accuracy and performance of this approach. This comparison assists users in identifying the strengths and weaknesses of numerical methods in solving nonlinear equations.
Advantages of Using the FTCS Method in CFD
- Simplicity of Implementation: The FTCS method is one of the simplest finite difference discretization methods, making it easy to implement and understand for CFD problems.
- Application in Preliminary Analyses: This method is suitable for initial analyses where high accuracy over a short period is required, effectively simulating nonlinear flows at early stages.
- Potential for Development and Improvement: This method can serve as a basis for comparison and evaluation of more complex methods, such as Lax or Lax-Wendroff.
Project Outputs and Key Features
- Access to Complete Fortran Code: All codes related to the FTCS method in Fortran, along with detailed explanations, are provided to users, enabling them to develop this algorithm based on their specific needs.
- Simulation Results and Numerical Analysis: The results from this simulation are presented in various tables and charts, allowing users to easily interpret the findings.
- Comprehensive Documentation: All implementation and analysis steps are thoroughly documented, including a step-by-step solution of the equation, setting boundary conditions, and results analysis.
Importance of This Project in CFD and Fluid Engineering
This project is suitable for students, researchers, and engineers seeking to understand numerical methods for solving fluid problems. Furthermore, the results can serve as a foundational model for more complex analyses and the development of advanced algorithms in CFD. Burgers’ Equation, as a simplified model of flow equations in fluids, can be used to convey essential concepts in turbulence and shock wave formation in real systems.