Project Overview
The Burgers’ equation, often known as the advection equation, is widely used in computational fluid dynamics and mathematical modeling to study nonlinear wave propagation, turbulence, and shockwave formation. This project focuses on solving both the linear and nonlinear forms of the Burgers’ equation using finite difference discretization. The solutions are developed for continuous and discontinuous initial conditions, providing a comprehensive approach to this essential fluid dynamics problem.
Numerical Methods Employed
To achieve accurate solutions, the project applies four advanced numerical methods, each with unique properties suitable for different aspects of the Burgers’ equation:
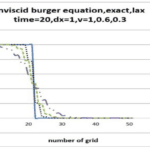
- Lax Method: This explicit finite difference scheme is well-known for its simplicity and stability when applied to hyperbolic partial differential equations. It serves as a baseline for comparison with other methods.
- Upwind Differencing Method: Ideal for capturing advective phenomena, the upwind method reduces numerical diffusion and is effective in handling discontinuities in initial conditions.
- Classical Lax-Wendroff Method: A second-order accurate scheme, the Lax-Wendroff method improves precision by considering temporal and spatial derivatives. This method is particularly useful for smoother solutions in nonlinear equations.
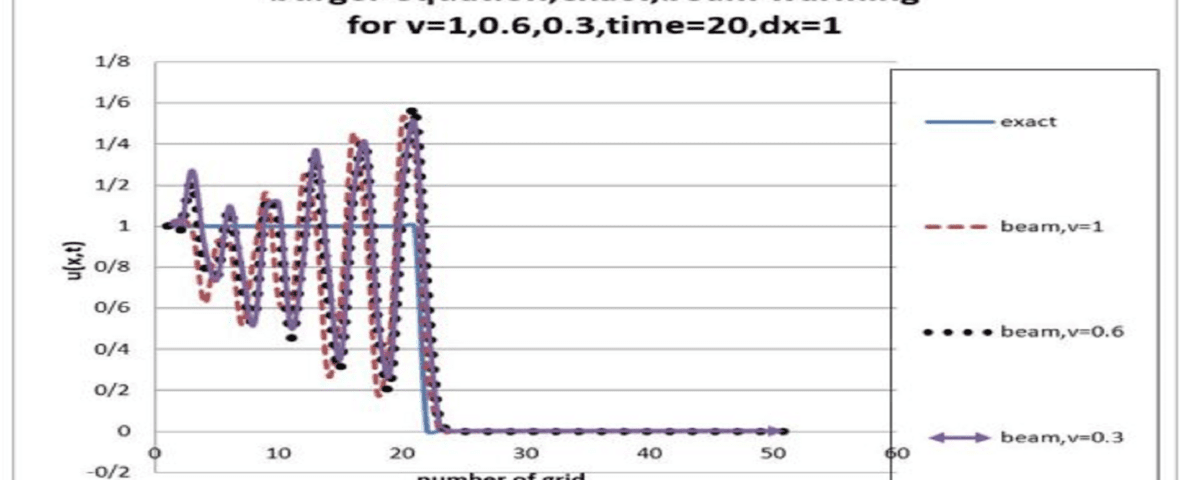
- Beam-Warming Method (Time-Centered or Trapezoidal Implicit): As an implicit method, the Beam-Warming technique is stable for larger time steps, making it suitable for solving equations with significant nonlinearity, such as the nonlinear Burgers’ equation.
Objective of the Project
The primary objective of this project is to solve the Burgers’ equation using the Beam-Warming method and compare the results with the exact analytical solution. This comparison allows for a detailed assessment of the method’s accuracy and effectiveness in capturing the dynamics of the equation.
Project Implementation in Fortran
All numerical methods and solution algorithms in this project are implemented using the Fortran programming language, known for its computational efficiency in scientific simulations. Upon acquiring this project, you will receive the complete Fortran code for each method, along with solution files and results.
Key Features and Deliverables
- Complete Code for All Methods: You will gain access to the Fortran code for the Lax, Upwind Differencing, Lax-Wendroff, and Beam-Warming methods.
- Results Comparison: Detailed comparisons with the exact solution to assess the performance and accuracy of each method.
- Documentation: Each code section is well-documented for easier understanding and adaptability to other equations and initial conditions.