Introduction
The Lax method is a numerical method used to solve partial differential equations, especially hyperbolic equations. Due to its simplicity and relative stability, it is used in many computational fluid dynamics (CFD) problems. The inviscid Burgers’ equation is a simple yet important equation in CFD that is used to model phenomena such as the formation of shock waves.
The general form of the Lax method for the inviscid Burgers’ equation is as follows:
u_i^(n+1) = 0.5 * (u_(i+1)^n + u_(i-1)^n) – 0.5 * (Δt/Δx) * (u_(i+1)^n)^2 + 0.5 * (Δt/Δx) * (u_(i-1)^n)^2
In this equation:
- u_i^(n) : Value of the function u at node i and time step n
- Δt : Time step
- Δx : Distance between nodes
The Inviscid Burgers equation is fundamental in fluid dynamics. It examines the nonlinear behavior of flows and describes phenomena such as shock formation. The Lax method is an effective numerical approach for solving this equation, offering high stability and accuracy. This project implements the Lax method in Fortran to solve the Inviscid Burgers equation. The study includes defining initial conditions, creating necessary matrices, and running numerical algorithms. This setup simulates time progression and provides valuable insights into computational fluid dynamics.
Conclusion
Computational Fluid Dynamics (CFD) analyzes fluid-related problems through numerical analysis and algorithms. This approach converts differential equations governing fluids into algebraic equations for numerical solutions. By dividing the analysis area into smaller elements and applying boundary conditions, a system of linear equations is created. Solving this system provides velocity, pressure, and temperature fields within the defined region.
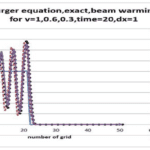
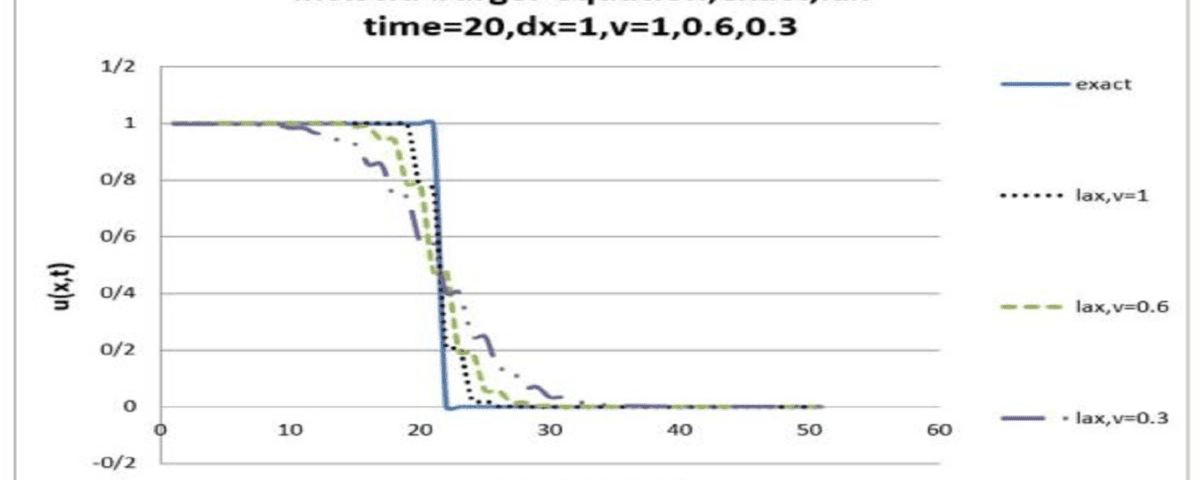
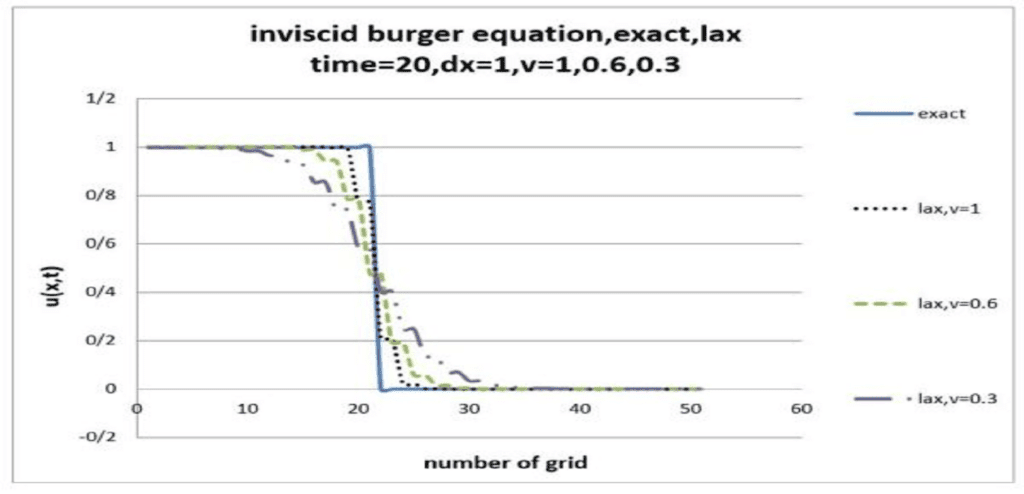
The goal of this project is to solve the Inviscid Burgers equation using the Lax method in CFD and to compare the results with exact solutions. The entire project, coded in Fortran, includes all solution methods and results.