Introduction
The heat equation, which describes heat transfer in various materials, is used in many engineering fields including mechanics, chemistry, and materials science. The Crank-Nicolson method is known as one of the efficient and accurate techniques in solving the heat equation. Because it offers a combination of implicit and semi-implicit methods, which leads to more stability and accuracy in the results. In this research, we will implement this method in Fortran programming language, including defining initial and boundary conditions, building matrices and performing numerical calculations for heat transfer analysis. The purpose of this study is to investigate the performance of the Crank-Nicolson method in simulating thermal phenomena and providing practical insights in the field of computational fluid dynamics.
Description
This method includes the time step with second-order accuracy and implicitly and is numerically stable. For diffusion equations (and many other equations) it can be proved that the crank nicolson method is unconditionally stable. However, its approximate solution can include significant fluctuations in the numerical solution if the ratio of the time step to the square of the spatial step is large (generally greater than half). It is one of the most widely used methods in simulating heat equations.
The purpose of this project is to solve heat equation with the computational fluid dynamics method (crank nicolson method) and compare the results with the exact solution. It should be mentioned that the entire project has been done with help of Fortran programming language. By preparing this project, the code of all the methods along with the results will be available to you.
Conclusion
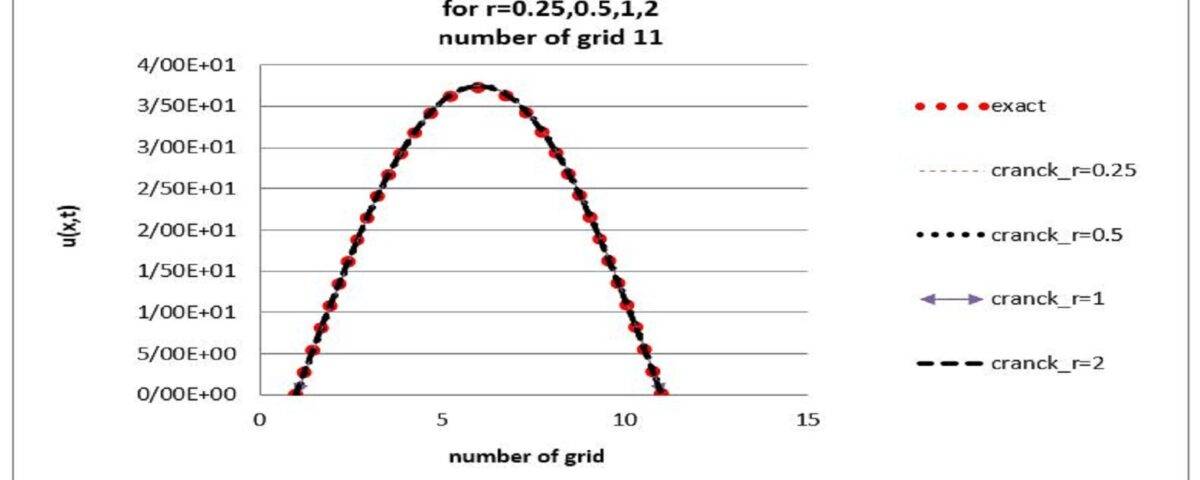
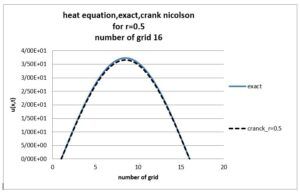
The Crank-Nicolson method, which offers a combination of accuracy and stability, allows for a more detailed analysis of heat transfer processes. Using specific initial and boundary conditions, simulations were performed that showed the thermal behavior of the system at different times.
This project not only helped to express the importance of using numerical methods in the analysis of thermal problems. Rather, it provided useful tools for future research in the field of computational fluid dynamics and heat transfer. Overall, this study emphasizes the application potentials of this method in engineering and materials science. And it opens the way for further investigations in the field of more complex issues.