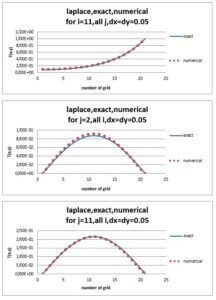
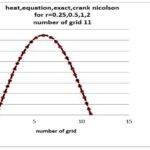
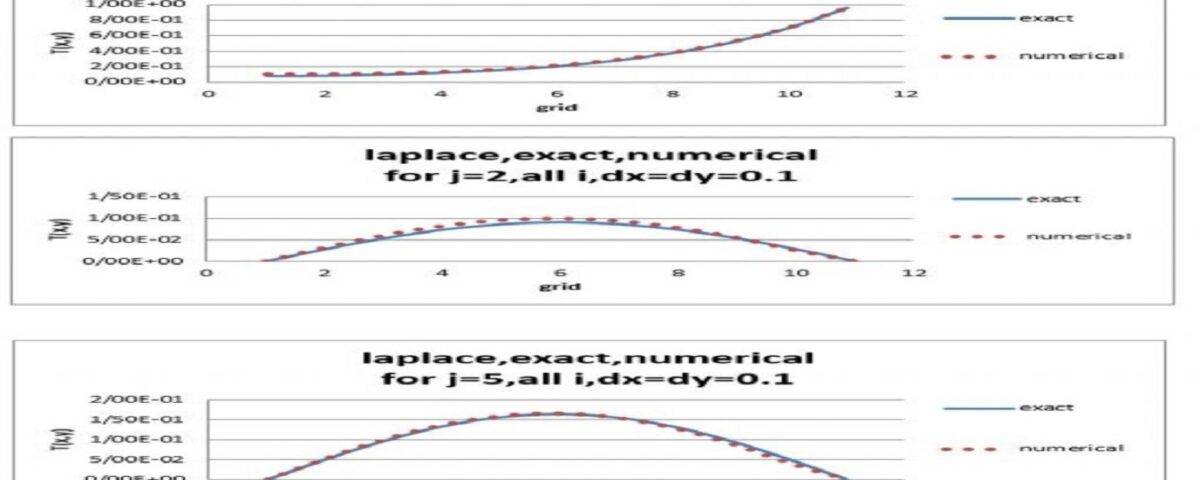
Description
Laplace’s equation is a very important partial differential equation in physics and engineering, widely used in problems related to physical potentials such as electric, gravitational, and ideal fluid flows. This equation states that the Laplacian of a scalar function is equal to zero.
Computational Fluid Dynamics (CFD) is a branch of engineering that uses numerical methods and algorithms to model and analyze fluid flow problems.
Relationship between Laplace’s Equation and CFD
Although Laplace’s equation does not appear directly in the governing equations of incompressible and viscous fluid flows (such as the Navier-Stokes equations), it can be used to solve various problems in CFD.
Some applications of Laplace’s equation in CFD include:
- Determining the pressure field: In incompressible flows, the pressure equation is Laplacian, and numerical methods can be used to solve it.
- Calculating the velocity potential: In potential flows, the fluid velocity is the gradient of a scalar function called the velocity potential. This velocity potential must satisfy Laplace’s equation.
- Solving heat transfer problems: Laplace’s equation is used in steady-state heat transfer problems to determine the temperature distribution.
- Solving electrostatic problems: Laplace’s equation is used to determine the electric field in free space.
Numerical Methods for Solving Laplace’s Equation in CFD
To numerically solve Laplace’s equation, various methods can be used, such as:
- Finite Difference Method: In this method, partial derivatives are approximated using the values of the function at discrete points.
- Finite Element Method: In this method, the domain of the problem is divided into smaller elements, and the unknown function in each element is approximated using basis functions.
- Finite Volume Method: In this method, the differential equation is discretized in a control volume, and the physical fluxes are calculated through the control surfaces.
Laplace’s equations are one of the most widely used equations in the science of heat transfer and fluid mechanics. Today, Computational Fluid Dynamics (CFD) is widely used to numerically solve Laplace’s equations. Therefore, it is essential for engineers and researchers in the field of heat transfer and fluid mechanics to be familiar with the methods of numerical solution of these types of equations and also to understand the relationships used in them. The purpose of this project is to solve Laplace’s equation with the computational fluid dynamics method and compare the results with the exact solution. It should be mentioned that the entire project has been done with the help of Fortran programming language. By preparing this project, the code of all the methods along with the results will be available to you.