Description
Partial Differential Equations (PDEs) are a group of differential equations involving unknown functions of several independent variables and their partial derivatives with respect to those variables. Differential equations have widespread applications in basic sciences such as mathematics, physics, chemistry, biology, and astronomy, as well as in engineering fields like mechanics, electrical engineering, materials science, and chemical engineering. These equations express the relationship between an unknown function of one or more independent variables and its various derivatives.
Many laws of nature are best expressed mathematically through differential equations. Since most real-world differential equations are non-linear and complex, finding analytical solutions for them is challenging. This has led to the development and expansion of numerical solution methods.
The most important criteria for evaluating numerical solution methods are speed, accuracy, and precision in solving equations. With significant improvements in the speed and capacity of information processing in computers, numerical solution methods have become more widespread, and this trend continues to grow.
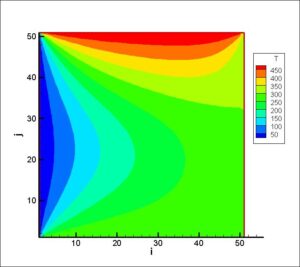
Solving The 2D Heat Transfer Equations of a Flat Plate in Two Ways in MATLAB
Partial Differential Equations (PDEs) are widely used to model phenomena in continuous environments, with common examples including wave and heat transfer equations. This project focuses on solving a two-dimensional heat transfer problem in a rectangular plate using both explicit and implicit methods. The solution is implemented using the Finite Difference method and programmed with MATLAB.