توضیحات
معادله لاپلاس یک معادله دیفرانسیل جزئی بسیار مهم در فیزیک و مهندسی است که به طور گسترده در مسائل مربوط به پتانسیل‌های فیزیکی مانند پتانسیل الکتریکی، گرانشی و جریان‌های سیال ایده‌آل استفاده می‌شود. این معادله بیان می‌کند که لاپلاسیان یک تابع اسکالر برابر با صفر است.
دینامیک سیالات محاسباتی (CFD) نیز شاخه‌ای از مهندسی است که با استفاده از روشهای عددی و الگوریتم‌ها، مسائل مربوط به جریان سیالات را مدل‌سازی و تحلیل می‌کند.
ارتباط معادله لاپلاس و CFD
اگرچه معادله لاپلاس به طور مستقیم در معادلات حاکم بر جریان سیالات تراکم‌ناپذیر و ویسکوز (مانند معادلات ناویر-استوکس) ظاهر نمی‌شود، اما می‌توان از آن برای حل مسائل مختلف در CFD استفاده کرد.
برخی از کاربردهای معادلات لاپلاس در CFD عبارتند از:
- تعیین میدان فشار: در جریان‌های تراکم‌ناپذیر، معادله فشار به صورت لاپلاسی است و می‌توان از روشهای عددی برای حل آن استفاده کرد.
- محاسبه پتانسیل سرعت: در جریان‌های پتانسیل (irrotational flows)، سرعت سیال گرادیان یک تابع اسکالر به نام پتانسیل سرعت است. این پتانسیل سرعت باید معادله لاپلاس را ارضا کند.
- حل مسائل مربوط به انتقال حرارت: معادله لاپلاس در مسائل انتقال حرارت حالت پایدار برای تعیین توزیع دما استفاده می‌شود.
- حل مسائل الکترواستاتیک: معادله لاپلاس برای تعیین میدان الکتریکی در فضای خالی استفاده می‌شود.
روشهای حل عددی معادله لاپلاس در CFD
برای حل عددی معادلات لاپلاس، از روشهای مختلفی مانند:
- روش تفاضل محدود (Finite Difference Method): در این روش، مشتقات جزئی با استفاده از مقادیر تابع در نقاط گسسته تقریب زده می‌شوند.
- روش اجزای محدود (Finite Element Method): در این روش، دامنه مسئله به عناصر کوچکتری تقسیم می‌شود و تابع مجهول در هر عنصر با استفاده از توابع پایه تقریب زده می‌شود.
- روش حجم محدود (Finite Volume Method): در این روش، معادله دیفرانسیل در یک حجم کنترل گسسته‌سازی می‌شود و شارهای فیزیکی از طریق سطوح کنترل محاسبه می‌شوند.
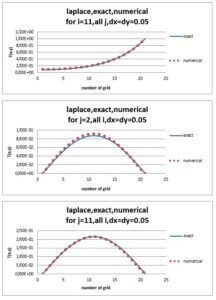
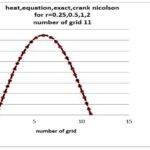
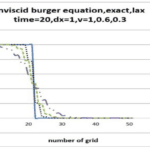
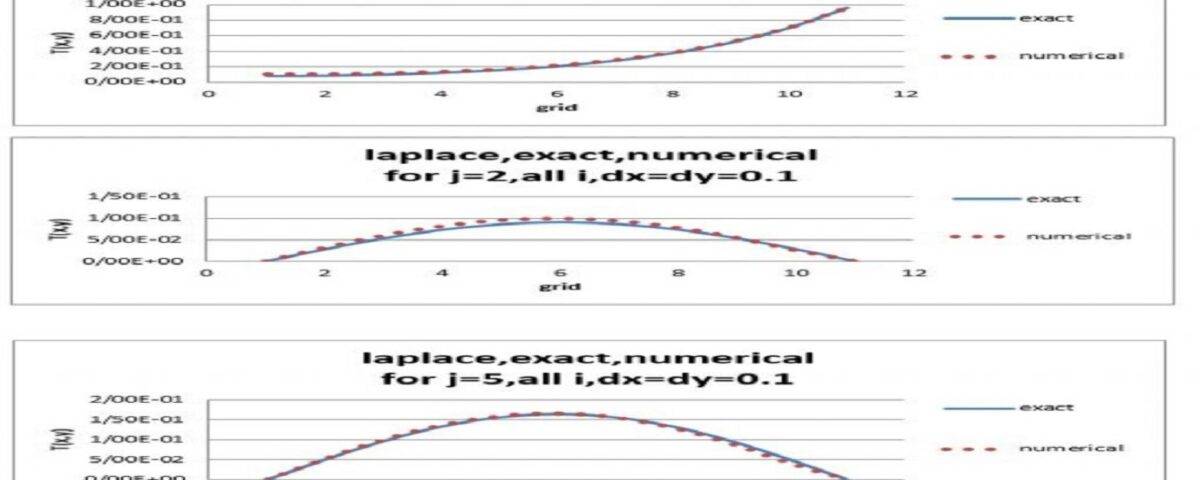
معادلات لاپلاس یکی معادلات پرکاربرد در علم انتقال حرارت و مکانیک سیالات می‌باشد. امروزه از دینامیک سیالات محاسباتی (CFD)، برای حل عددی معادلات لاپلاس به صورت چشمگیری استفاده می شود. بنابراین آشنایی با روشهای حل عددی این نوع معادلات و نیز درک روابط به کاررفته در آن برای مهندسان و محققان حوزه انتقال حرارت و مکانیک سیالات امری ضروری می باشد. هدف از انجام این پروژه حل معادله لاپلاس با روش دینامیک سیالات محاسباتی و مقایسه ی نتایج حاصل از آن با حل دقیق می باشد. لازم به ذکر تمامی پروژه به کمک زبان برنامه نویسی فرترن انجام شده است. با تهیه این پروژه کد تمامی روشها به همراه نتایج حاصل از آن در اختیار شما قرار خواهد گرفت.
جهت خرید این پروژه و یا کسب اطلاعات بیشتر از طریق لینک زیر اقدام فرمایید.